|
Antes de proceder a resolver un
sistema de ecuaciones lineales, tenemos que dar respuesta a las siguientes
preguntas: ¿El sistema tiene
solución, es decir, es compatible? En caso afirmativo: ¿Tiene una solución o infinitas?
Para responderlas, una de las herramientas que podemos utilizar es la que
proporciona el Teorema de
Rouché-Fröbenius, cuyo enunciado es el siguiente:
Consideremos un sistema de m ecuaciones lineales con n
incógnitas, cuya expresión general
es la siguiente:

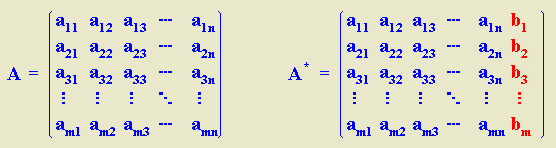
Sean A la matriz del sistema
y A* la matriz ampliada del sistema (con los
términos independientes).
La
condición necesaria y suficiente para que un sistema de m ecuaciones lineales
con n incógnitas sea compatible es que el rango de la matriz de los
coeficientes de las incógnitas (A) sea igual al rango de la matriz ampliada
con los términos independientes (A*). Es decir: rango (A) = rango (A*).
Si el
valor común de los rangos coincide con el número de incógnitas, el sistema es
compatible determinado. Si, por el contrario, el valor de los rangos es menor
que el número de incógnitas el sistema es compatible indeterminado.
En resumen:
Un caso particular es el de los
sistemas homogéneos, es decir,
aquellos en los que todos los términos
independientes son nulos.
Pues, en este caso, las matrices A
y A* son semejantes a efectos
del cálculo del rango, dado que la matriz A* es la matriz A
a la que se le añade una columna de ceros, que podemos suprimir para calcular
el rango. Por lo tanto, siempre se cumple que rango (A) = rango (A*). Esto quiere decir que todos los sistemas homogéneos son siempre compatibles. Se cumple:
Una vez realizada la
"discusión o identificación del sistema", aplicaremos alguno de los
métodos que desarrollaremos en los epígrafes posteriores. No obstante, es
preciso tener en cuenta las siguientes observaciones:
|
miércoles, 28 de marzo de 2012
TEOREMA DE ROUCHE
jueves, 22 de marzo de 2012
TIPOS DE MATRICES
En matemáticas, se denomina matriz a un conjunto ordenado de
números, ubicados en una estructura de filas y columnas. Estas cantidades pueden
sumarse, multiplicarse y descomponerse de variadas maneras.
Existen distintos tipos de matrices:
MATRIZ FILA: es un tipo de matriz conformada por una única fila.
MATRIZ COLUMNA: esta clase de matriz se conforma por una sola columna.

MATRIZ RECTANGULAR: se caracteriza por presentar un número diferente de filas
que de columnas. Su dimensión es m x n.
MATRIZ CUADRADA: presenta la misma cantidad de filas que de columnas. Los
elementos que van desde la esquina superior izquierda hacia la esquina inferior
derecha constituyen la diagonal principal.

MATRIZ NULA: recibe este nombre debido a que esta conformada por todos ceros
como elementos.
MATRIZ TRIANGULAR SUPERIOR: en esta clase de matriz los elementos ubicados
por debajo de la diagonal superior son ceros.
MATRIZ TRIANGULAR INFERIOR: aquí los elementos colocados por encima de la
diagonal principal son ceros.
MATRIZ DIAGONAL: esta clase de matriz cuenta con la particularidad de que la
totalidad de los elementos ubicados tanto por encima de la diagonal como por
debajo de ella son nulos.

MATRIZ ESCALAR: es el nombre que recibe aquella matriz diagonal en la cual
los elementos que conforman la diagonal principal son iguales.
MATRIZ IDENTIDAD: en este tipo de matriz los elementos que componen la
diagonal principal son iguales a 1.

MATRIZ TRASPUESTA: a partir de una matriz A, se denomina matriz traspuesta de
A, a aquella matriz que se obtiene al cambiar de manera ordenada las filas por
las columnas.

MATRIZ REGULAR: se denomina de esta manera a aquella matriz cuadrada que
tiene inversa.
MATRIZ SINGULAR: es un tipo de matriz que no posee inversa.
BIBLIOGRAFIA
sábado, 3 de marzo de 2012
OPERACIONES CON MATRICES
AQUI ESTA EL LINK PARA QUE DESCARGUEN LA DIAPOSITIVA
https://skydrive.live.com/redir.aspx?cid=60f01ef353d390c7&resid=60F01EF353D390C7!107&parid=60F01EF353D390C7!103&authkey=!AGygvP6Gu5uqZwY
https://skydrive.live.com/redir.aspx?cid=60f01ef353d390c7&resid=60F01EF353D390C7!107&parid=60F01EF353D390C7!103&authkey=!AGygvP6Gu5uqZwY
BIOGRAFIA DE KARL FRIEDRICH GAUSS
Karl Friedrich Gauss
 |
| Karl Friedrich Gauss |
El duque le proporcionó asistencia financiera en sus estudios secundarios y universitarios, que efectuó en la Universidad de Gotinga entre 1795 y 1798. Su tesis doctoral (1799) versó sobre el teorema fundamental del álgebra (que establece que toda ecuación algebraica de coeficientes complejos tiene soluciones igualmente complejas), que Gauss demostró.
En 1801 Gauss publicó una obra destinada a influir de forma decisiva en la conformación de la matemática del resto del siglo, y particularmente en el ámbito de la teoría de números, las Disquisiciones aritméticas, entre cuyos numerosos hallazgos cabe destacar: la primera prueba de la ley de la reciprocidad cuadrática; una solución algebraica al problema de cómo determinar si un polígono regular de n lados puede ser construido de manera geométrica (sin resolver desde los tiempos de Euclides); un tratamiento exhaustivo de la teoría de los números congruentes; y numerosos resultados con números y funciones de variable compleja (que volvería a tratar en 1831, describiendo el modo exacto de desarrollar una teoría completa sobre los mismos a partir de sus representaciones en el plano x, y) que marcaron el punto de partida de la moderna teoría de los números algebraicos.
Su fama como matemático creció considerablemente ese mismo año, cuando fue capaz de predecir con exactitud el comportamiento orbital del asteroide Ceres, avistado por primera vez pocos meses antes, para lo cual empleó el método de los mínimos cuadrados, desarrollado por él mismo en 1794 y aún hoy día la base computacional de modernas herramientas de estimación astronómica.
En 1807 aceptó el puesto de profesor de astronomía en el Observatorio de Gotinga, cargo en el que permaneció toda su vida. Dos años más tarde, su primera esposa, con quien había contraído matrimonio en 1805, falleció al dar a luz a su tercer hijo; más tarde se casó en segundas nupcias y tuvo tres hijos más. En esos años Gauss maduró sus ideas sobre geometría no euclidiana, esto es, la construcción de una geometría lógicamente coherente que prescindiera del postulado de Euclides de las paralelas; aunque no publicó sus conclusiones, se adelantó en más de treinta años a los trabajos posteriores de Lobachewski y Bolyai.
Alrededor de 1820, ocupado en la correcta determinación matemática de la forma y el tamaño del globo terráqueo, Gauss desarrolló numerosas herramientas para el tratamiento de los datos observacionales, entre las cuales destaca la curva de distribución de errores que lleva su nombre, conocida también con el apelativo de distribución normal y que constituye uno de los pilares de la estadística.
Otros resultados asociados a su interés por la geodesia son la invención del heliotropo, y, en el campo de la matemática pura, sus ideas sobre el estudio de las características de las superficies curvas que, explicitadas en su obra Disquisitiones generales circa superficies curvas (1828), sentaron las bases de la moderna geometría diferencial. También mereció su atención el fenómeno del magnetismo, que culminó con la instalación del primer telégrafo eléctrico (1833). Íntimamente relacionados con sus investigaciones sobre dicha materia fueron los principios de la teoría matemática del potencial, que publicó en 1840.
Otras áreas de la física que Gauss estudió fueron la mecánica, la acústica, la capilaridad y, muy especialmente, la óptica, disciplina sobre la que publicó el tratado Investigaciones dióptricas (1841), en las cuales demostró que un sistema de lentes cualquiera es siempre reducible a una sola lente con las características adecuadas. Fue tal vez la última aportación fundamental de Karl Friedrich Gauss, un científico cuya profundidad de análisis, amplitud de intereses y rigor de tratamiento le merecieron en vida el apelativo de príncipe de los matemáticos.
"bajado desde"
Suscribirse a:
Entradas (Atom)